和 Usenet.nl 的糾紛(解決篇)
Mon, 13 Sep 2010 21:36:44 +0800 | Comments(125) | Category:Consumption | Tags:consumption dispute usenet.nl
在我認為準備已經足夠後,我立刻就啟動了 PayPal 的 dispute report,方法如下:
- 登入 PayPal
- 開啟 My Account 的子項目 Resolution Center
- 點選按鈕 Dispute a Transaction
- 到這裡你會看到兩個選項:Item dispute 和 Unauthorized transaction
我之前遲遲不動作就是卡在這裡,照直覺來看應該選 Unauthorized transaction,但是我看了官方的說明後又覺得不太對。在 PayPal 的文件裡,這個項目比較像是處理帳號盜用的問題。在我的情況,Usenet.nl 事實上是有我的授權的,只是雙方對契約的認知上出現了差異,因而產生糾紛。我請別人幫我判斷,他告訴我兩個方法應該都可以,不過 Item dispute 可能要拖的比較久,因此我最後選擇 Unauthorized transaction。接下來:
- 進到 Unauthorized transaction 後 PayPal 要求你填寫 unauthorized transaction ID,你可以點選欄位旁的按鈕,它會開啟你的交易清單。你只要點選你想要申訴的交易的 ID,系統就會自動把 ID 幫你填上。
- 按下 Continue 之後,來到最後一個部份。這時候 PayPal 會要你提供一些相關資訊。其中最重要的是最後一欄:2000 字以內的陳述。當你都填妥後,你的申訴手續就完成了,再來就等 PayPal 的回應。
這裡附上我寫的陳述
The cause of this dispute is my disagreement about how Usenet.nl charged me.
On 8 August 2010, I registered myself on Usenet.nl, and chose to use a test period. At that time, I paid them 1 € through PayPal. I had no intention to continue to use their service after this test period then.
Later on 23 August 2010, I received your notification of this transaction in surprise, and I immediately went back to the website of Usenet.nl and review their TOS(Term Of Service) carefully. In their TOS, it says if the Customer didn't cancel within the test period, the contract will extend automatically. This is why this transaction happened.I must admit, I didn't pay much attention to their TOS when I registered, this is my fault. However, I think Usenet.nl also has the responsibility in helping their Customer to understand their TOS, but I don't feel they fulfilled it. The following is my reasons:
- In addition to their TOS, Usenet.nl didn't give any sufficient warning about the "extend automatically", they didn't mail me any notification before they charged me, either. This, I felt, is unacceptable.
- Before my case, there have been several similar disputes with Usenet.nl, I found these complains on internet:
I don't have any solid evidence, though. However, some of the users also paid the charge through PayPal, so I think you might have some dispute reports about Usenet.nl, and that would support my claim.
- http://www.complaintsboard.com/complaints/usenetnl-c341714.html
- http://bozonessinc.ca/2010/06/the-blogs-response-to-usenet-nl/
- http://www.ripoffreport.com/internet-services/usenet-nl/usenet-nl-very-sneaky-and-dec-76aca.htm
Since I wasn't the first with this problem, I think they should have known their test period scheme would cause disputes potentially, but they didn't remedy it.I hope these reasons would grant me a fully refund and I am willing to provide any further information if needed.
Thanks for your help.
這並不是最原始的版本,我稍微做了一些修正。
我是在深夜提交的,PayPal 隔天早上就結案了,它通知我會把費用完整的退回我的信用卡裡。我真的覺得 PayPal 的效率非常了不起,也十分感謝它能認同我的觀點,讓我能取得退費。
希望我的經驗能幫到那些發生相同問題的人。
和 usenet.nl 的糾紛
Sun, 29 Aug 2010 06:35:46 +0800 | Comments(199) | Category:Consumption | Tags:consumption dispute usenet.nl
8/23 早上打開 gmail,赫然發現 paypal 來了一封通知,我的帳戶支付了一筆四千多元的款項給 usenet.nl。
時間回到 8/8,兩個星期前,研究室的同學不小心把存有重要資料的硬碟給格式化了,為了幫他救回資料,我上網找尋磁碟救援的軟體。經過一番搜尋後連到了 usenet.nl,它是一個可以讓用戶共享資料的平台,你可以在它所有的使用者之間搜尋你要的檔案,當然,你必須為這項服務支付費用。
我稍微看了 usenet.nl 的說明,它為新的使用者提供了一項試用的方案,以 1€ 的代價取得為期 14 天的試用及 5G 的下載配額。我很快的完成了註冊,並以 paypal 支付了 1€ 的費用,很快地 usenet.nl 啟動了我新註冊的帳號。之後我順利的完成了磁碟救援的工作(但這並不是因為 usenet.nl 的關係),我便把這件事拋諸腦後了。
收到 paypal 來的通知讓我大吃一驚,我已為我和 usenet.nl 的關係已經結束了,怎麼它又多收了一筆費用呢?我趕緊再到 usenet.nl 的網站上重新查看它的使用條款(term of service, TOS),在條款的第六項寫著:
Art. 6 Start of the contractual term, tariffs, authorisation for automatic access, term of the contract, cancellation
6.1. The contract between the Supplier and the Customer will be concluded for the contractually agreed term.
If the Customer should only choose to use a test period with his Registration, the contractual term will begin at the start of the test period.
Without a cancellation, the contract will extend automatically by a selected term, if it has not been cancelled by later than one (1) days prior to expiry of the contractual term.
In addition to cancellation in writing or by e-mail, the Customer also always has the opportunity to cancel a subscription directly online at usenet.nl. A refund entitlement to the payments made during the selected and confirmed contractual term is also excluded in this case.
另外,在第八項也寫著:
Art. 8 Cancellation right and test period
8.3. If the Customer should not cancel within the test period, the contract will extend automatically by the time period selected and confirmed upon conclusion of the contract. The Customer can only use the test period once, unless the Supplier explicitly permits the Customer an additional test period.
看到這裡事情的原因總算清楚了。usenet.nl 的使用條款假定用戶會在試用期間過後續約,因此若用戶沒有在試用結束前主動中止合約,usenet.nl 會自動延長合約成期限一年,每個月有 25G 下載配額的標準方案,費用是 99.96€,換算成台幣約四千多元。
雖然這個事件主要是由於我的疏忽所造成,但總覺得 usenet.nl 的作法讓我不太能接受,我在網路上搜尋了一會兒,發現我並不是第一個有這樣問題的人,我這裡列出一些其它網友的抱怨
- usenet.nl Complaints - fraud
- usenet.nl Complaints - Injustice
- Usenet.nl is a Scam
- The Blogs Response to Usenet.nl
- usenet.nl Review | Rip-off Report #545776
整合了這些資料,我以如下的理由為我自身的利益做辯護:
在這樣的契約中,使用者有義務主動了解 usenet.nl 訂定的使用條款,但是 usenet.nl 也有責任協助使用者了解使用條款,特別是那些容易引起糾紛的部分;我認為 usenet.nl 在這方面並沒有完全盡責。一方面,類似的事件並不是第一次發生,usenet.nl 應該知道它這樣的做法有引起紛爭可能性;另一方面,對於自動延長合約,usenet.nl 只有在我註冊時以使用條款的方式告知,在我試用的期間,usenet.nl 都沒有再做額外的通知。這樣不完善的做法讓我難以信服。
我決定在 paypal 上提出對 usenet.nl 的糾紛申訴,希望能有一個好的結果。
用 it's all text! 編輯 is-programmer post: 請小心
Sun, 29 Aug 2010 06:06:39 +0800 | Comments(3206) | Category:Computer | Tags:computer is-programmer
今天不小心把誤刪了一個 post。
習慣上,我都是用 firefox 的 plugin: it's all text! 配合 vim 在 ubuntu 下以 source code 的方式編寫 post。有好一段時間沒寫 post 了,為了重新熟悉 html 的語法,我在寫新的 post 的同時還開了一篇舊的 post 做參考。沒想到 it's all text! 在存檔時把舊的 post 的 source code 給覆寫了,我又一不留神的按了存檔,於是之前寫的 real analysis 作業就少了一篇。
下次要特別小心,再發生一次我可受不了。
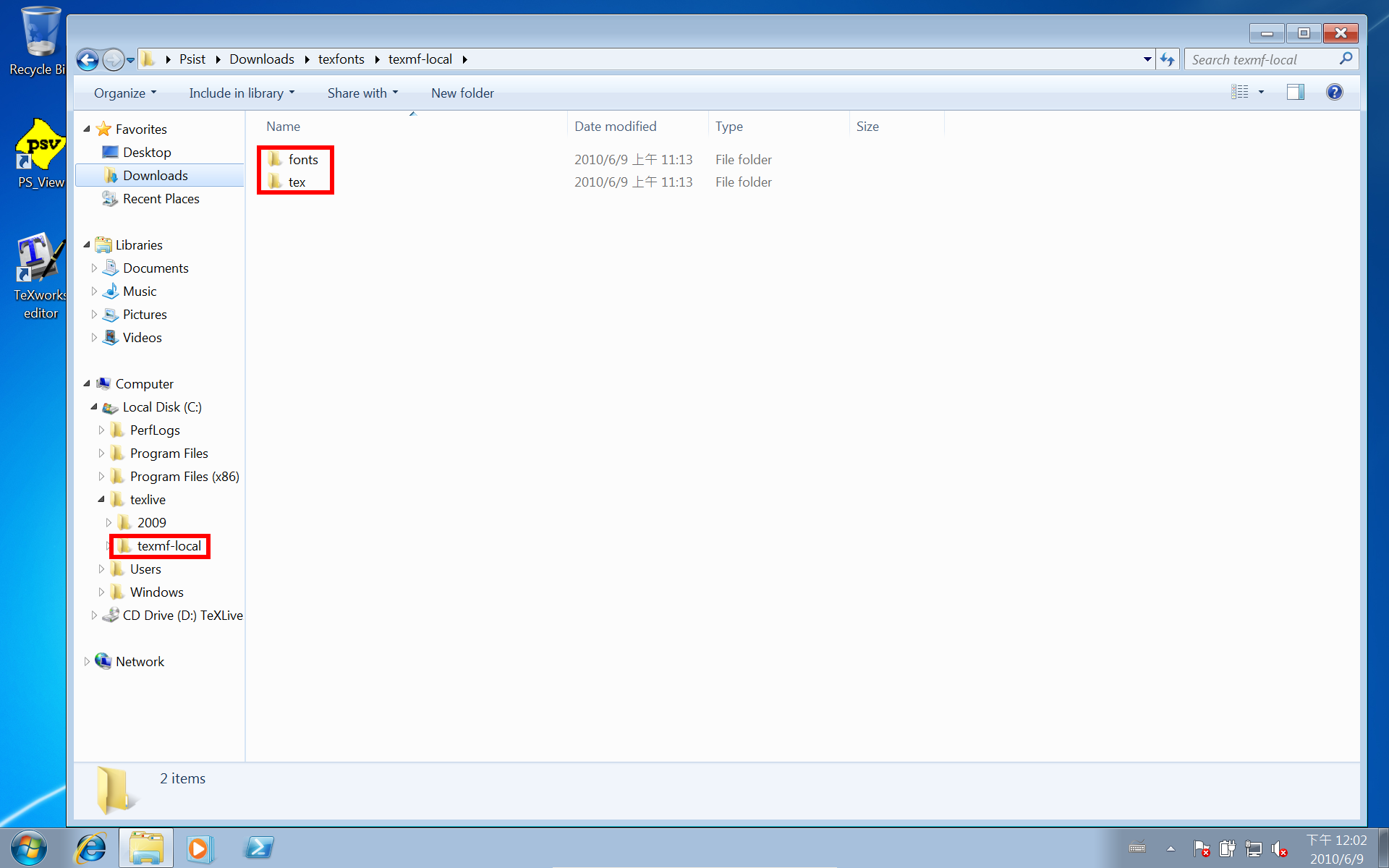
如何在 Windows 下使用 LaTeX
Tue, 08 Jun 2010 17:36:13 +0800 | Comments(2558) | Category:Computer | Tags:computer latex
在 Linux 用慣了 TeXLive,因此我打算在 Windows 下還是用 TeXLive。
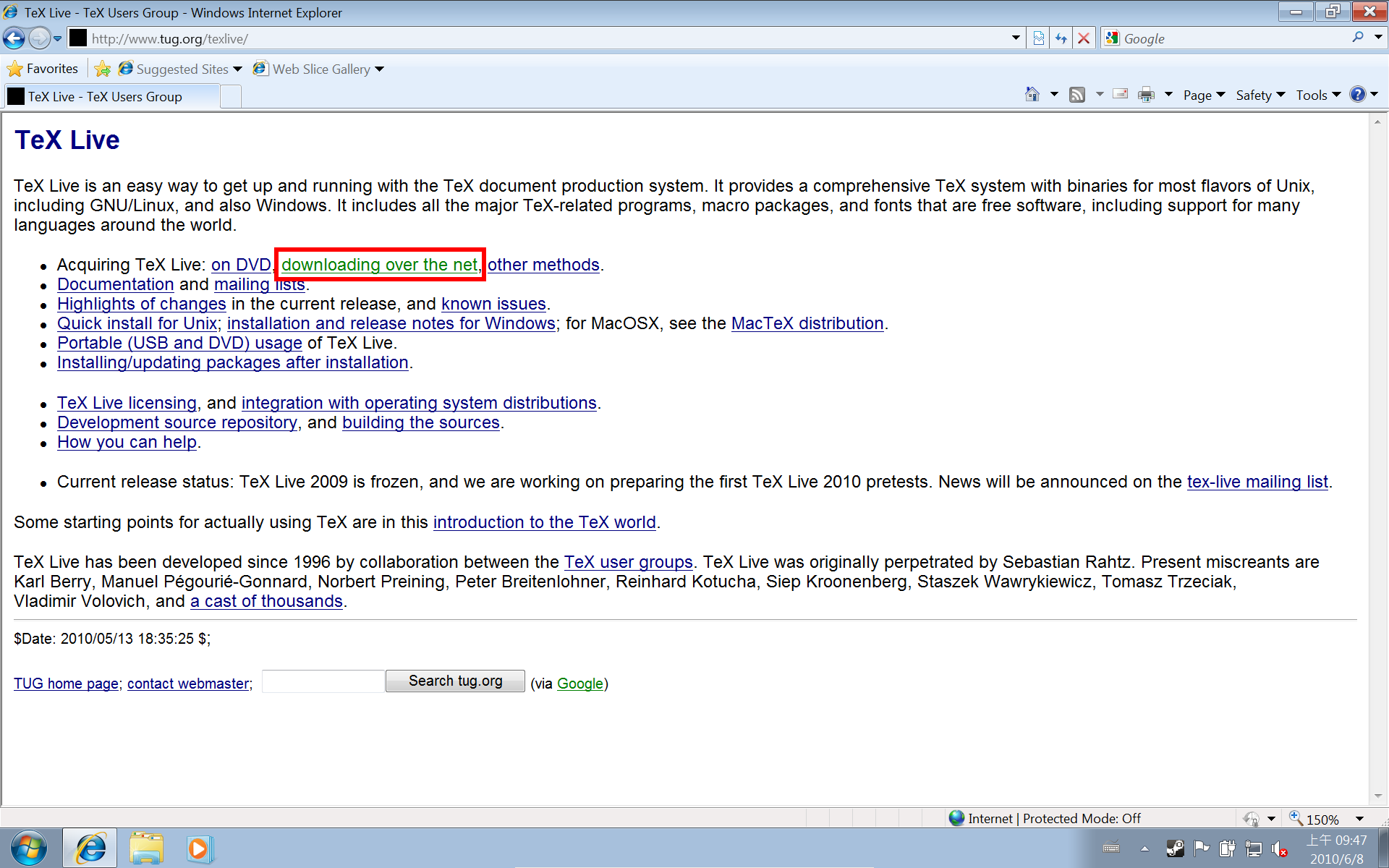
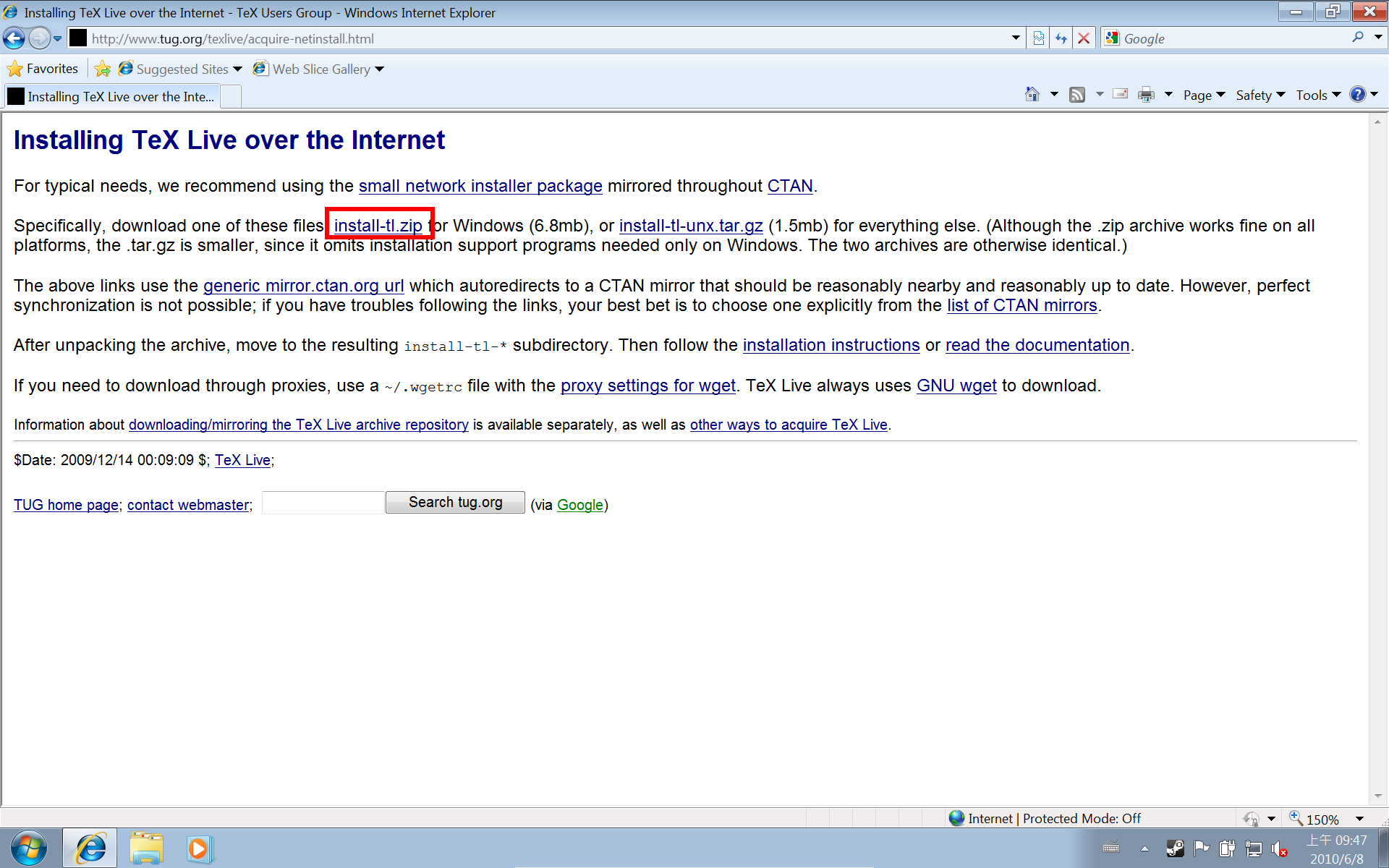
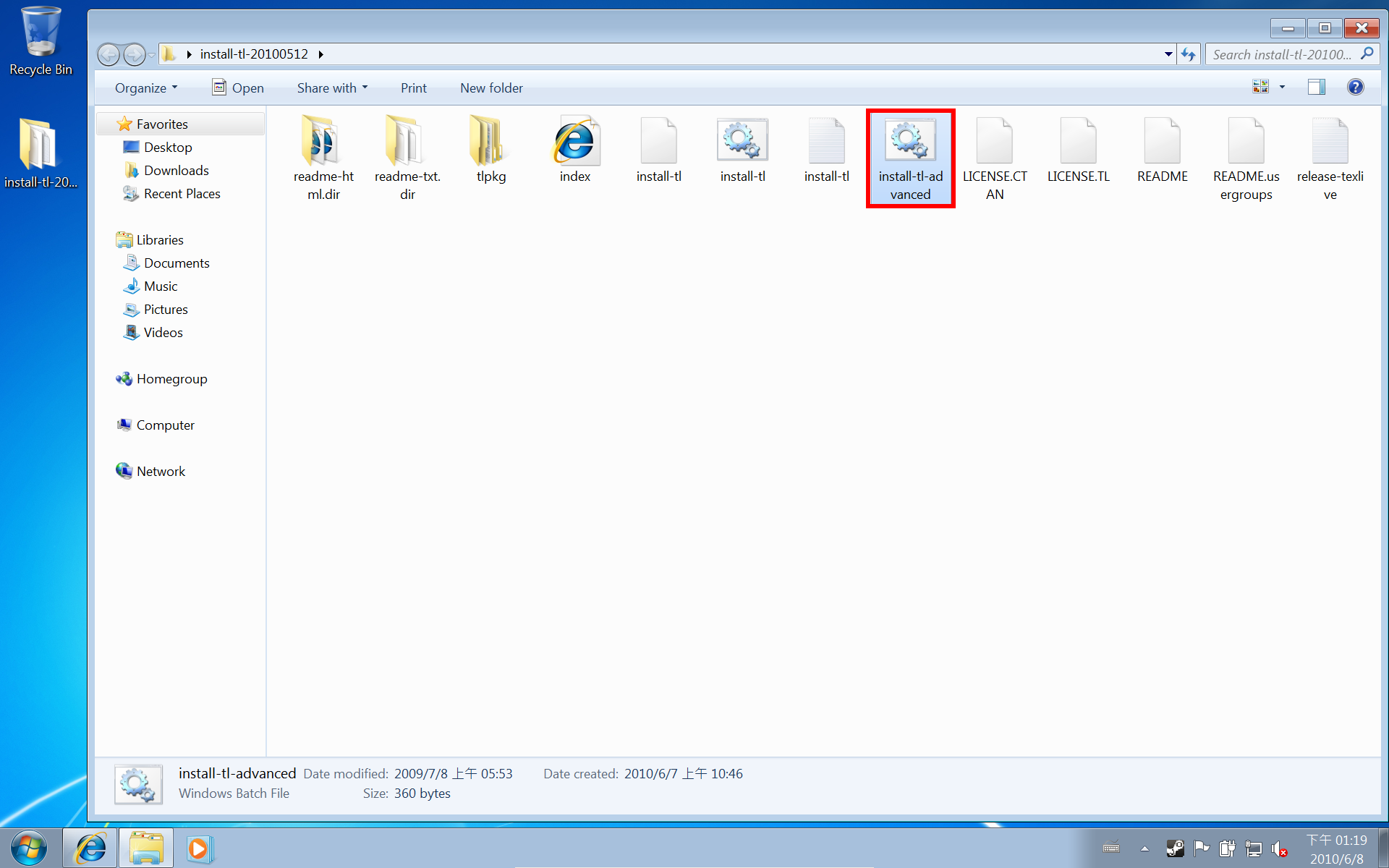
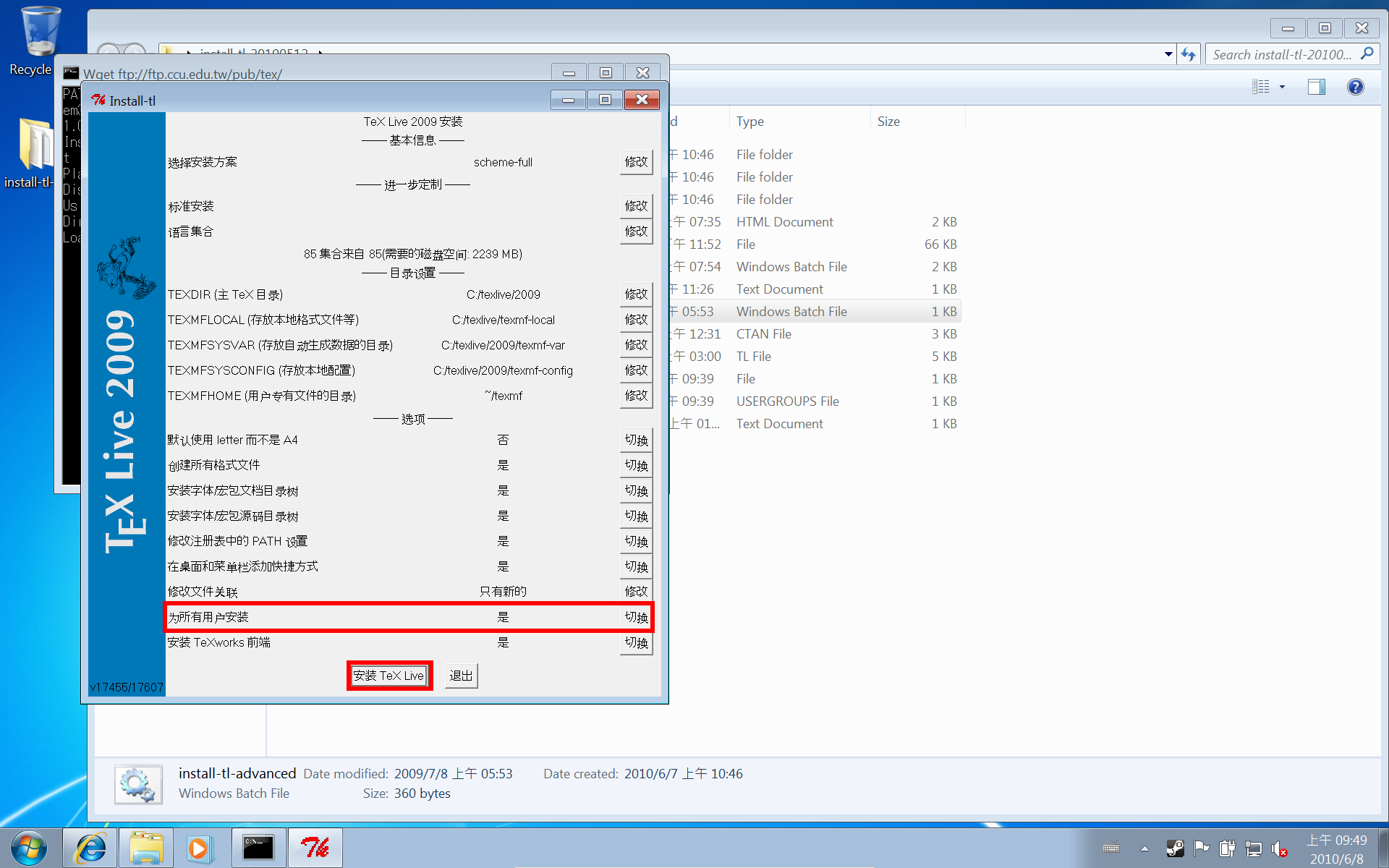
先連到 TeXLive 的官方網站:http://www.tug.org/texlive/,按下面的圖進行操作。
接著,開啟終端機執行
texhash updmap --enable Map=nsungu.map updmap --enable Map=cwmu.map updmap --enable Map=cwyu.map updmap --enable Map=cwku.map updmap --enable Map=cwhbu.map updmap --enable Map=cwfsu.map
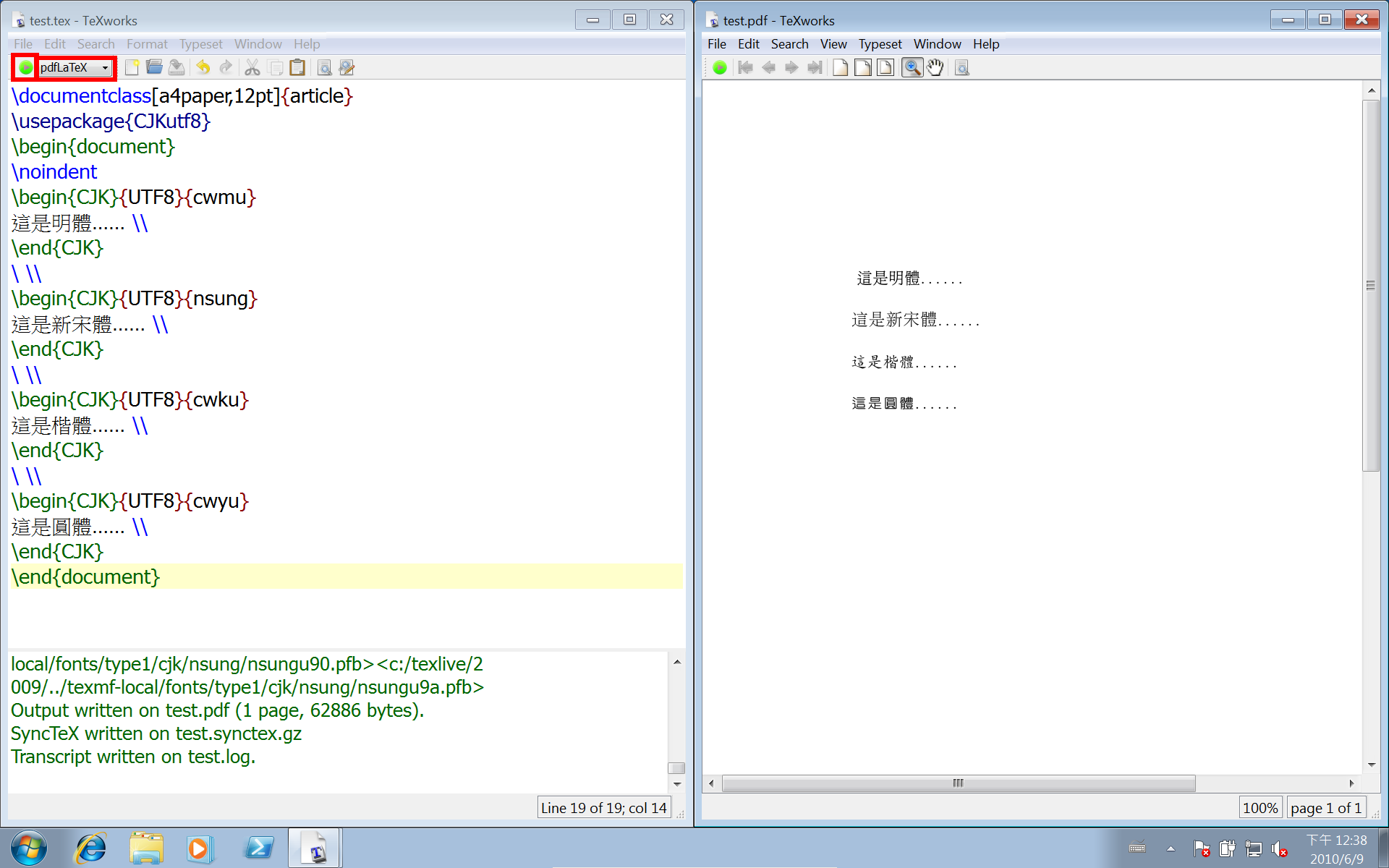
完成後測試看看
最後,中文字型檔 下載
Real Analysis HW 04-26 (II)
Fri, 21 May 2010 06:31:41 +0800 | Comments(863) | Category:Math | Tags:math real_analysis
Let [tex]f[/tex] be a continuous function on [tex]\mathbb{R}^n\backslash\{0\}[/tex] that is homogeneous of degree [tex]-n[/tex] (i.e., [tex]f(rx)=r^{-n}f(x)[/tex]) and has mean zero on the unit sphere (i.e., [tex]$\int f\ d\sigma=0$[/tex] where [tex]\sigma[/tex] is surface measure on the sphere). Then [tex]f[/tex] is not locally integrable near the origin (unless [tex]f=0[/tex]), but the formula
(Hint: For any [tex]a>0[/tex], the indicated limit equals
-
I'll show first that [tex]f[/tex] is not locally integrable near the origin. Given any [tex]r>0[/tex], consider
[tex] \begin{align*} \int_{\left\lvert x\right\rvert\leq r}{\left\lvert f(x)\right\rvert\ dx}&= \int_{s=0}^r\int_{\left\lvert x\right\rvert=s}{\left\lvert f(x)\right\rvert\ d\sigma ds}\\&=\int_{s=0}^r s^{-1}\ ds\ \int_{\left\lvert x\right\rvert=1}{f(x)\ d\sigma}. \end{align*} [/tex]
-
Next I'll show that [tex]\mathrm{PV}(f)\in \mathcal{D}'[/tex]. Given [tex]\phi\in C_c^\infty(\mathbb{R}^n)[/tex] and [tex]\epsilon>0[/tex], then
[tex] \begin{align*} &\int_{\left\lvert x\right\rvert>\epsilon}{\left\lvert f(x)\phi(x)\right\rvert\ dx}\\\leq\quad&\int_{\epsilon<\left\lvert x\right\rvert\leq 1}{\left\lvert f(x)\right\rvert\left\lvert\phi(x)-\phi(0)\right\rvert\ dx}+\int_{\left\lvert x\right\rvert>1}{\left\lvert f(x)\right\rvert\left\lvert\phi(x)\right\rvert\ dx}\\=\quad&\mathrm{I}+\mathrm{II} \end{align*} [/tex]For part I,[tex] \begin{align*} \mathrm{I}&=\int_{\epsilon<\left\lvert x\right\rvert\leq 1}{\left\lvert f(x)\right\rvert\left\lvert x\cdot \nabla\phi(\xi(x))\right\rvert\ dx}\\&\leq\sup\left\lvert\nabla\phi\right\rvert\ \int_{\epsilon<\left\lvert x\right\rvert\leq 1}{\left\lvert x\right\rvert\left\lvert f(x)\right\rvert\ dx}\\&=\sup\left\lvert\nabla\phi\right\rvert\ \int_{s=\epsilon}^1 ds\ \int_{\left\lvert x\right\rvert=1}{\left\lvert f(x)\right\rvert\ d\sigma}\\&\leq\sup\left\lvert\nabla\phi\right\rvert\ \int_{\left\lvert x\right\rvert=1}{\left\lvert f(x)\right\rvert\ d\sigma}. \end{align*} [/tex]On the other hand, for part II,[tex] \begin{align*} \mathrm{II} \leq\left\lvert\mathrm{supp}\ \phi\right\rvert\sup_{x\in\mathbb{R}^n}{\left\lvert\phi(x)\right\rvert}\ \sup_{\left\lvert x\right\rvert\geq 1}{\left\lvert f(x)\right\rvert}. \end{align*}[/tex]
-
From the estimate above, by dominated convergence theorem, [tex]\mathrm{PV}(f)[/tex] is indeed a distribution.
The remaining is obvious.
Real Analysis HW 04-26 (I)
Wed, 19 May 2010 21:52:46 +0800 | Comments(219) | Category:Math | Tags:math real_analysis
A distribution [tex]F[/tex] on [tex]\mathbb{R}^n[/tex] is called homogeneous of degree [tex]\lambda[/tex] if [tex]F\circ S_r=r^\lambda F[/tex] for all [tex]r>0[/tex], where [tex]S_r(x)=rx[/tex].
- [tex]\delta[/tex] is homogeneous of degree [tex]-n[/tex].
- If [tex]F[/tex] is homogeneous of degree [tex]\lambda[/tex], then [tex]\partial^\alpha F[/tex] is homogeneous of degree [tex]\lambda-\left\lvert\alpha\right\rvert[/tex]
- The distribution [tex](d/dx)[\chi_{(0,\infty)}(x)\log x][/tex] discussed in the text is not homogeneous, although it agree on [tex]\mathbb{R}\backslash\{0\}[/tex] with a function that is homogeneous of degree [tex]-1[/tex].
- Recall the fact that if [tex]T:\mathbb{R}^n\rightarrow\mathbb{R}^n[/tex] is an invertible linear transform, then
[tex]\begin{align*} \int f(x)\ dx &= \int f\circ T(x)\ dT(x) \\ &= \det(T)\int f\circ T(x)\ dx. \end{align*}[/tex]This simple example helps us understand how composition of a distribution with an invertible linear transform behaves.
- For a, consider that given any [tex]\phi\in C_c^\infty(\mathbb{R}^n)[/tex],
[tex]\begin{align*} \left<\delta\circ S_r,\phi\right>&=\det(S_r)^{-1} \left<\delta,\phi\circ {S_r}^{-1}\right> \\ &=r^{-n}\left<\delta,\phi\right>. \end{align*}[/tex]
- For b, consider that given an [tex]F\in\mathcal{D}'[/tex] which is homogeneous of degree [tex]\lambda[/tex], then for any [tex]\phi\in C_c^\infty(\mathbb{R}^n)[/tex] we have
[tex]\begin{align*} \left<\partial^\alpha F\circ S_r,\phi\right>&= \det(S_r)^{-1}\left<\partial^\alpha F,\phi\circ {S_r}^{-1}\right>\\ &=r^{-(n+\left\lvert\alpha\right\rvert)}\left<F, (-1)^{\left\lvert\alpha\right\rvert}\partial^\alpha\phi\circ {S_r}^{-1}\right>\\ &=r^{-\left\lvert\alpha\right\rvert}\left<F\circ S_r,(-1)^{\left\lvert\alpha\right\rvert}\partial^\alpha\phi\right>\\ &=r^{\lambda-\left\lvert\alpha\right\rvert}\left<F,(-1)^{\left\lvert\alpha\right\rvert}\partial^\alpha\phi\right>\\ &=r^{\lambda-\left\lvert\alpha\right\rvert}\left<\partial^\alpha F,\phi\right> .\end{align*}[/tex]
- For c, as same as text, we define
[tex]\begin{align*} L_\epsilon(x)=\chi_{(\epsilon,\infty)}(x)\log x \end{align*}[/tex]for some [tex]\epsilon>0[/tex].
Given any [tex]\phi\in C_c^\infty(\mathbb{R})[/tex], we have[tex]\begin{align*} \left<{L_\epsilon}'\circ S_r,\phi\right>&=r^{-2}\left<L_\epsilon,-\phi'\circ {S_r}^{-1}\right>\\ &=r^{-1}\left<L_\epsilon\circ S_r,\phi'\right>\\ &=r^{-1}\left<(\log r+\log x)\chi_{(\epsilon/r,\infty)},-\phi'\right> \end{align*}[/tex]If we let [tex]\epsilon\rightarrow 0[/tex], then the equation above becomes[tex]\begin{align*} \left<L'\circ S_r,\phi\right>&=r^{-1}\left<\log r\ \delta+L',\phi\right> \end{align*}[/tex]Therefore, [tex]L'[/tex] is not homogeneous.
LaTeX Test
Wed, 19 May 2010 15:47:39 +0800 | Comments(376) | Category:Test | Tags:test
Consider [tex]z\in\mathbb{C}[/tex], define
Perfect!看來可以跟 blogger 說再見了。